【学習メモ】グラフ理論入門の入門

0.はじめに

大学でグラフ理論を勉強する機会があったので学んだことを書きなぐっていきます。グラフ理論は情報工学界隈に限らず、広く一般的に使われている学問領域です。また今回取り上げる内容は表題のとおり、入門中の入門ということで聞いたことがあるという方もいらっしゃることかもしれません。とはいえ、グラフ理論を勉強していくうちにその魅力にとりつかれ、しっかり学んで血となり肉としたいと思い、自分のために勉強したことを書き残していきます。

cf. 帝京大学理工学部(通信教育課程)の社会人大学生1年目をふりかえる | gkzz.dev

1.前提

グラフ理論を勉強する難しさをあげるとしたら、書籍やウェブサイトなど資料によって、「同じことを言っているが、使っている用語が異なる」、さらには「用語のスコープが異なる」こと
- e.g. ノードと同じ意味：節点、頂点、点
- e.g. エッジと同じ意味：枝、辺、線
そこで、本ページではいわゆる用語の定義は参考資料を掲載する程度としたい
本書の位置づけは、「グラフ理論を勉強するとどういった用語を目にすることになるのか？」という、グラフ理論入門の入門とする

2.「グラフ理論」でいわれている「グラフ」とは？

ノードの集合とエッジの集合を用いて様々な現象をモデル化したもの
ノードは節点、頂点、点ともいう
エッジは枝、辺、線ともいう
- 株価チャートのようなものではない
- 数字が連続的ではなく、「飛び飛び（離散的）」

2-1.「グラフ」を使って抽象化された一例

電車の乗換案内アプリ
- 電車の乗換案内アプリを使う目的は、現在地から目的地までの最短経路を知ること
- ただし、「コスト（グラフ理論的には『重み』）」をキョリ、交通費、交通機関の乗り換え回数などどれにするか？ によって答えは変わる！

2-2.グラフの構成要素であるノードやエッジは電車の乗換案内アプリでは、どれに該当するか

ノード：駅
エッジ：線路や駅と駅を結ぶ道路
重み：移動コスト（キョリ、交通費、交通機関の乗り換え回数など）

参考:

3.「グラフ理論」を勉強するとなにがうれしいか

検討対象が膨れ上がってしまうような 「組み合わせ爆発」が起きてしまう問題に対する「向き合い方」 をおさえておくことができる！
- 後述するオイラーグラフ、ハミルトングラフなど典型的なグラフ構造は、離散的アプローチをするうえでの武器となる
- いわゆる「一筆書きできるかどうか」の判断も、ルートをしらみつぶしに調べ上げることなくできる

4.「グラフ」の基本的な考え方

※ 用語説明は以下の書籍と動画に譲りたい。ここではグラフに対する基本的な考え方、見方を挙げていく。

離散数学入門#6: オイラーグラフと郵便配達員問題 - 00:06:41
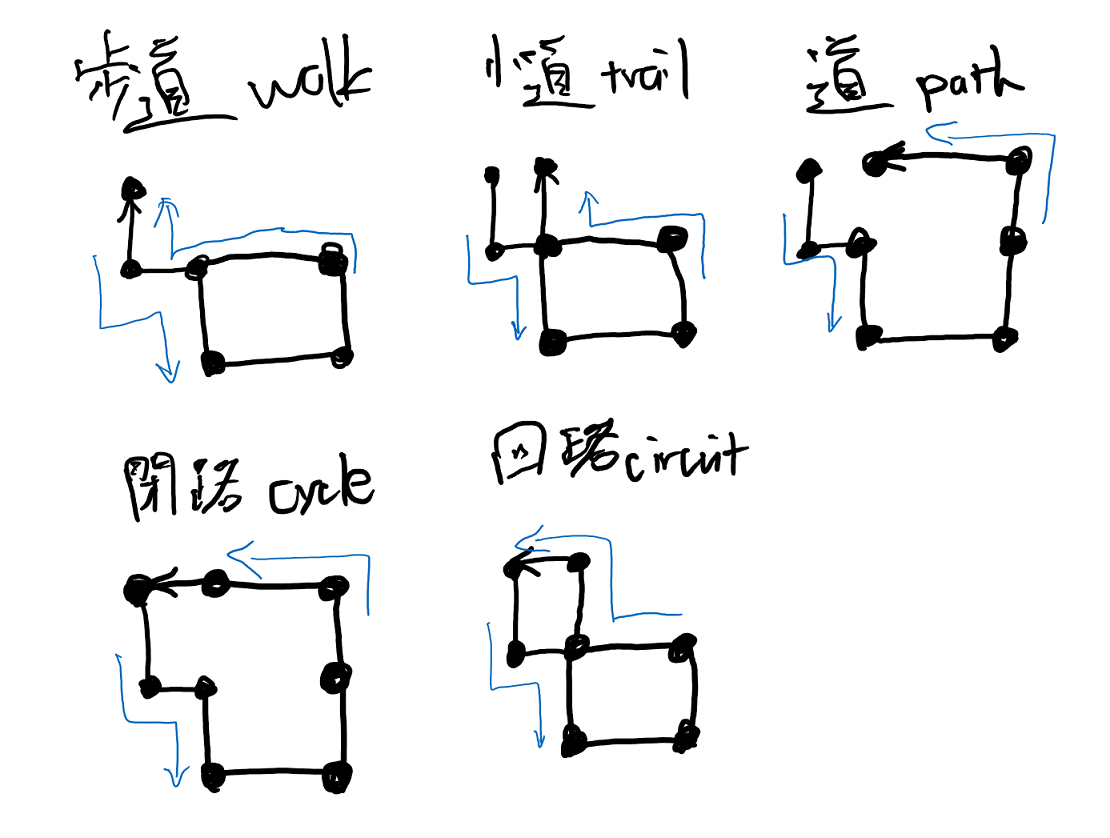
- 歩道(walk)、小道(trail)、道(path)、閉路(cycle)の類似点と相違点について図を用いて分かりやすく解説されていて、おすすめ
例題で学ぶグラフ理論 | 安藤清, 土屋守正, 松井泰子 |本 | 通販 | Amazon
- 上記の講義動画シリーズで推薦されていた書籍の一つ。他の書籍より自分にはこれが合っていた。
- 離散数学入門#0: グラフ理論へのイントロダクション，授業ガイダンス・基本的な用語の準備

* 歩道(walk): 頂点から始まり、頂点と辺が交互に結び、頂点で終わる列（頂点や辺の重複があってもよい）
* 小道(trail): 辺の重複がない歩道(頂点の重複があってもよい)
* 道(path): 辺の重複がない歩道のうち、頂点の重複がないもの
* 閉路(cycle): 辺の重複がない歩道のうち、「始点と終点以外」頂点の重複がないもの（始点と終点は重複している）
* 回路(circuit): 閉じた小道。辺の重複がない歩道のうち「始点と終点が重複」しているもの

※ 図は離散数学入門#6: オイラーグラフと郵便配達員問題 - 00:06:41を参考に筆者作成

4-1.グラフは同形であるか

「同形」と字面だけ読むと、「合同」や「相似」のことかと思ってしまうが違う
同形である場合は以下のことを指す（全て満たす必要があると思っている。また、用語の正確な意味、スコープは上述したとおり、割愛したい。）
- ノードやエッジの数が同じである
- ノードが隣接している（隣り合っているか）
- 次数が同じノードが隣接している
- ※次数とは、ノードに接続するエッジの本数

4-2.一筆書きできるか(もれなくだぶりなくエッジを通ることが出来るか)

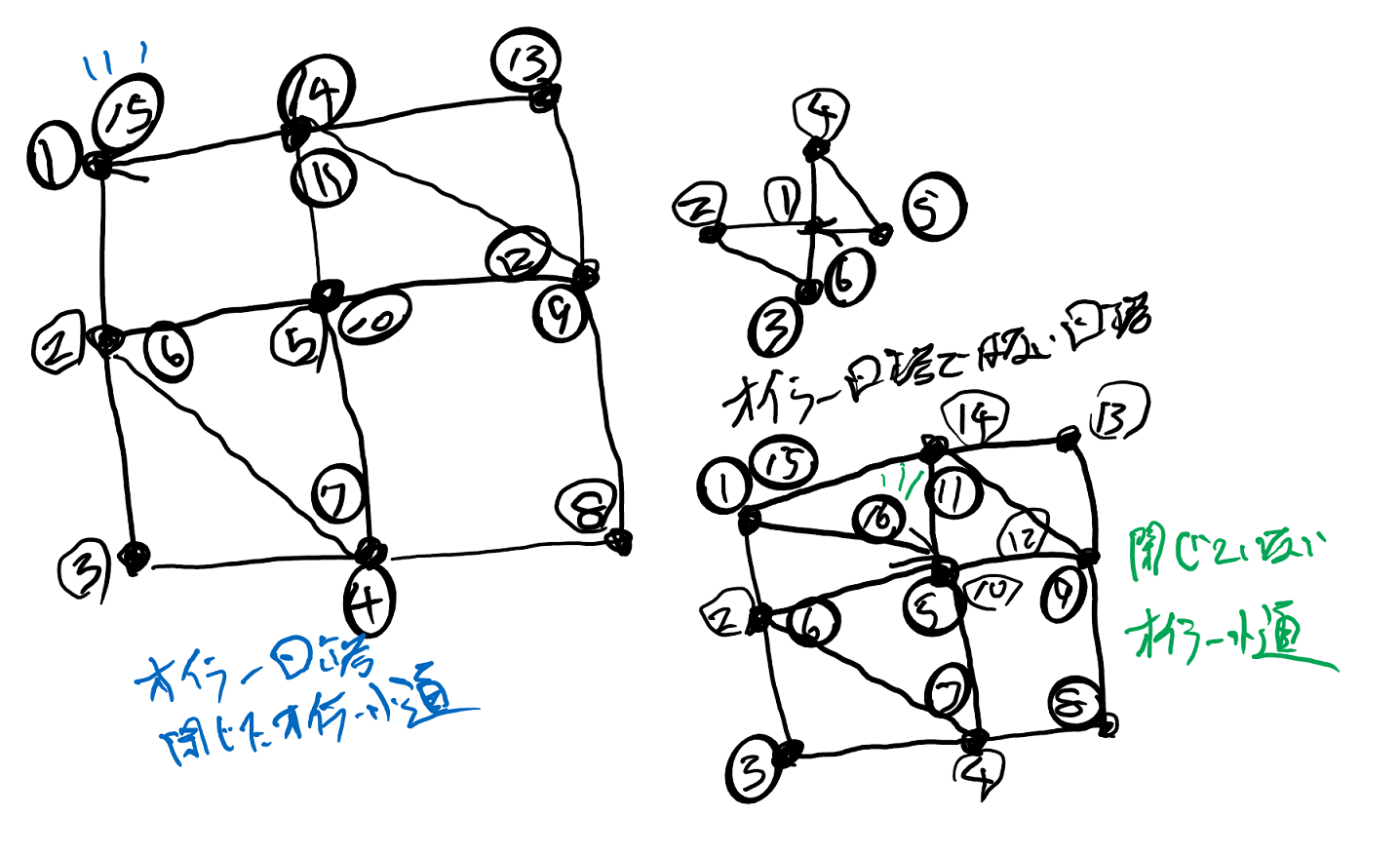
オイラーグラフ
- 各ノード（節点、頂点、点）は偶点
- 各ノード（節点、頂点、点）の次数は偶数
- 各ノード（節点、頂点、点）に接続するエッジの本数が偶数個！

※ 準オイラーグラフの特徴は、奇点が2個であること（オイラーグラフの奇点は0）。「巡回はできないけど、一筆書きはできる。」

画像の出所：Eulerian path - Wikipedia

※ 図は離散数学入門#6: オイラーグラフと郵便配達員問題 - 00:08:55を参考に筆者作成

4-3.もれなくだぶりなくノードを通ることができるか

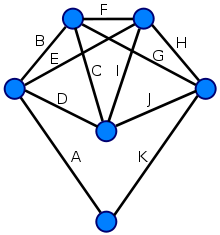
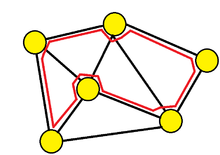
ハミルトングラフ
- オイラーグラフと違い、カンタンに判定が出来る定理、必要十分条件がない

画像の出所：Hamiltonian path - Wikipedia

5.章にまとめるほどでもなかったけど書き留めておきたい小ネタ

更新する際に章を設けるかも

グラフ理論周辺の学問領域とは

大学数学への展望 | 高校数学の美しい物語

「グラフ理論」に関連するトピック

ケーニヒスベルクの橋の問題とは - コトバンク
六次の隔たり - Wikipedia
複雑ネットワーク - Wikipedia
- 現実世界に存在するネットワークは多様であり、巨大で複雑な構造を有しているが、一定の共通する性質を見出すことができる。それらの性質は「スケールフリー性」（次数分布のべき乗則）、「スモールワールド性」、「クラスター性」と呼ばれている。

X.参考

帝京大学理工学部(通信教育課程)の社会人大学生1年目をふりかえる | gkzz.dev

0.はじめに#

1.前提#

2.「グラフ理論」でいわれている「グラフ」とは？#

2-1.「グラフ」を使って抽象化された一例#

2-2.グラフの構成要素であるノードやエッジは電車の乗換案内アプリでは、どれに該当するか#

3.「グラフ理論」を勉強するとなにがうれしいか#

4.「グラフ」の基本的な考え方#

4-1.グラフは同形であるか#

4-2.一筆書きできるか(もれなくだぶりなくエッジを通ることが出来るか)#

4-3.もれなくだぶりなくノードを通ることができるか#

5.章にまとめるほどでもなかったけど書き留めておきたい小ネタ#

グラフ理論周辺の学問領域とは#

「グラフ理論」に関連するトピック#

X.参考#